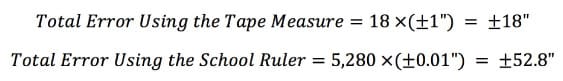Imagine you are given the task to measure the length of the street you live on, and you are only allowed to use either a tape measure or a school ruler. Which one would be your choice?
In this, the 2nd post in our five-part series on Measuring Success, we explore the essential question all analysts should ask themselves before approaching any problem: what’s the best tool to use? Going back to our example, we know that we have higher precision using the school ruler (let’s assume that precision for the school ruler is ±0.01” versus ±1” for the tape measure). But, does that mean the school ruler is the right choice?
Some simple math could give us the answer. A normal school ruler is 12 inches while a typical tape measure is 300 ft. So, if your street is about a mile, you have to use the full length of tape measure about 18 times. However, in case of using the school ruler that number rises to 5,280 times. You might think that the point is: “it is definitely faster and more convenient to use the tape measure and that is why we should choose the tape measure over the school ruler.” But, what if speed was not an issue?
An analogy of that in today’s analytics world is that computers are so fast that it really does not matter if I choose “school ruler” over “tape measure”. Nevertheless, we should not forget that, overall, the street is long enough that the tape measure would give us an even more accurate estimate of the street length than the school ruler.
We see that not only using the tape measure is faster, but will also give us more accurate results. However, if the length of your street was about one hundredth of a mile, then the school ruler would have given you more accurate results. Yet, you still might spend a lot of time and end up with major backache just for the sake of slightly more accuracy in measuring a length that could be measured using a tape measure only once.
That is why analysts should pick their choice of aggregation level of observations used in their models based on the final accuracy level that they expect from those models, not on the accuracy level that they gain from the choice of their observations, e.g. your weekly forecast is less volatile than your daily forecast.
NOTES:
- In the example presented in the post, the measurement error is the combination of tool accuracy (we don’t have tape measures or rulers that have tick marks for every possible granular unit) and user error. However, for the sake of simplicity let’s assume that user error is ZERO here. Either way we have two devices which give us ±0.01” and ±1” of error in each measurement they are used.
- Now, if we have to measure something that is 6” which is less than the length of both devices, we still will end up with the same amount of error we get in a full measurement. That is why when we divide the length of the street by the length of the devices, we have to ROUNDUP that number to get the number of measurements.
- A full mile is 5280 ft. So, 1.88% of the full mile has a length of 99.264 ft, which requires 100 times of measurement using the ruler and one measurement using the tape measure. That is our break-even point between the two devices when it comes to total error.
NEXT WEEK’S POST: RIGHT INTERPRETATION
Error: Contact form not found.